Roger Penrose (n. 1931, Colchester, Inglaterra/Reino Unido), matemático muito conhecido de Oxford (cadeira Emérita Rouse Ball), foi agraciado hoje pelo comitê do Prêmio Nobel de Física por seu trabalho que mostrou que a Teoria Geral da Relatividade de Einstein implicava a existência de buracos negros, no interior dos quais as leis da Física deixariam de funcionar.
Interessante notar que Einstein não acreditava na existência dos buracos negros, mas faleceu cerca de 10 anos antes de Penrose publicar seus resultados.
Penrose estudou primeiramente com W. V. D. Hodge, conhecido pelo operador de Hodge, que fornece o adjunto da diferencial usual (para uma métrica Riemanniana) e permite a definição do operador de Laplace-Hodge, é fundamental para o estudo da cohomologia de Georges de Rham, mas terminou sua tese sobre métodos tensoriais em geometria algébrica sob John A. Todd.
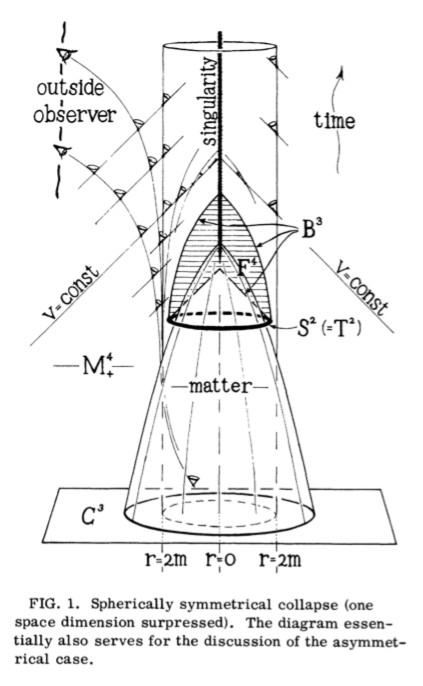
Seu trabalho fundamental sobre as relações entre a Teoria Geral da Relatividade e a existência de buracos negros foi publicada em 1965, no artigo “Gravitational Collapse and Space-Time Singularities“, que introduziu métodos topológicos no estudo da cosmologia.
O artigo tem apenas duas páginas e meia e uma figura, que está ao lado. O ponto chave do resultado foi mostrar que não era necessário assumir nenhuma simetria para se obter a singularidade que geraria o buraco negro, como era o caso de todos os exemplos até então estudados. Nas palavras do próprio Penrose, sublinhadas no artigo, “Será mostrado que,…, desvios da simetria esférica não podem evitar singularidades no espaço-tempo de ocorrerem“.
Penrose trabalhou em muitas outras áreas da matemática, inclusive em reticulações do plano, criando as “Penrose tilings”. Correspondeu-se com M. Escher, o grande artista holandês, que utilizou algumas das ideias de Penrose em suas gravuras, principalmente o “triângulo de Penrose”, que deu origem à famosa gravura de Escher da escada circular.
Leia e veja mais: Prêmio Nobel de Física 2020 Notícia na BBC Entrevista (BBC) Gravuras impossíveis de Escher



