Sala de aula: o Teorema Fundamental do Cálculo

A ideia: o Teorema Fundamental do Cálculo (TFC) estabelece a relação entre as duas principais construções que definem o conteúdo do Cálculo Diferencial e Integral e que estão incluídas no próprio nome dessa área da matemática, a derivada e a integral. Ele nos diz que essas duas construções são inversas uma da outra, de uma forma bem clara e explícita, matematicamente.

O que faremos: essa breve exposição busca esclarecer essa correspondência, introduzindo os conceitos relevantes e o enunciado do teorema em suas duas formas, apresentar uma demonstração bem simples e alguns exemplos interessantes, mostrando a importância dos resultados, e indicar como o teorema se generaliza para outras situações. Ao final, temos alguns comentários históricos, sobre como o TFC surgiu, ao final do século 17, com Newton e Leibniz, e porque seu desenvolvimento levou séculos a acontecer.

A derivada

Recordamos que a derivada surge quando se define a taxa de variação instantânea de uma função $f:A \subseteq \mathbb{R} \longrightarrow \mathbb{R}$ , que se obtém da variação média da função em um intervalo da variável independente quando fazemos esse intervalo tender a um ponto (intervalo de comprimento nulo) através do uso do limite, que é o conceito fundamental do cálculo.

Como motivação, pensemos no caso de um corpo cuja distância em relação ao ponto de saída (tempo igual a zero) é descrita pela função $d=f(x)$ , dada em metros ( $m$ ), e $x=t$ é o tempo, dado em segundos ( $s$ ). Assim, a velocidade média $v_{\textrm{média}}(t_1,t_2)$ entre os valores de tempo $t_1$ e $t_2$ seria a distância percorrida, $\Delta d= f(t_2)-f(t_1)$ , dividida pelo tempo transcorrido, $\Delta t = t_2-t_1$ ,

$v_{\textrm{média}}(t_1,t_2) = \frac{\Delta d}{\Delta t} = \frac{f(t_2)-f(t_1)}{t_2-t_1},$

que teria como unidades $m/s$ . Agora, tomamos o processo de limite, fazendo $t_2$ tender a $t_1$ , isto é, consideramos o intervalo de tempo ficando cada vez menor, com $\Delta t$ tendendo a zero. Esse processo, quando possível, nos dá a velocidade instantânea em $t_1$ ,

$v(t_1) = \lim_{t_2 \rightarrow t_1} v_{\textrm{média}}(t_1,t_2)= \lim_{t_2\rightarrow t_1}\frac{f(t_2)-f(t_1)}{t_2-t_1}=\lim_{\Delta t \rightarrow 0}\frac{\Delta d}{\Delta t}.$

Essa velocidade instantânea é a derivada da função $f(x)$ no ponto $x=t_1$ , que podemos escrever como

$f^\prime(t_1) = \frac{df}{dx}(t_1)=\lim_{x\rightarrow t_1}\frac{f(x)-f(t_1)}{x-t_1}.$

A diferença entre essa expressão é a que nos dá a velocidade instantânea acima está apenas no uso da variável original $x$ em vez de pensar no intervalo de tempo $[t_1,t_2]$ que está sendo comprimido fazendo $t_2\rightarrow t_1$ . A definição da derivada permite considerar intervalos em que o ponto de interesse, $t_1$ , possa ser tanto o extremo inferior do intervalo considerado (o caso $[t_1,x]$ ), como o extremo superior (o caso $[x,t_1]$ ). O limite na expressão da derivada considera as duas possibilidades, simultaneamente, e essa é a definição usual de derivada (e de velocidade instantânea).

A integral

Para motivar a integral, consideramos a mesma situação, do movimento de um corpo, só que agora temos sua velocidade em cada instante de tempo, que denotamos por $v(x)$ , onde $x=t$ é o tempo ( $s$ ), e $v(x)$ é dado em $m/s$ . Vamos supor, primeiramente, que a posição do corpo no instante inicial ( $t_0=0$ ) é a origem $d=0$ sobre uma reta que tem uma escala marcada em metros ( $m$ ).

Consideremos o caso mais simples, em que a velocidade instantânea é constante, isto é $v(x) = v_0$ , para todos os valores de tempo $x=t$ . Nesse caso, sabemos que a distância percorrida entre os instantes $t_0=0$ e $t>0$ será simplesmente o produto da velocidade (constante) pelo intervalo de tempo transcorrido,

$d(t) = v_0 \Delta t = v_0 (t-t_0) = v_0 t.$

Assim, temos que a velocidade constante ( $v=v_0$ ) no fornece um movimento em que a distância cresce linearmente, na forma $d(t) = v_0 t$ . Se a posição inicial não for a origem, mas a posição $d_0$ , e o instante de tempo inicial for um valor também dado $t_0$ , que pode ser igual a zero ou não, a posição em função do tempo seria dada pela equação

$d(t) = d_0 + v_0 (t-t_0) ,$

que é a equação mais geral de uma reta.

Note que $v_0$ é a inclinação desta reta, que é a motivação geométrica para a definição da derivada. Ou seja, se derivarmos $d(t)$ em relação a $t$ , obtemos $v_0$ , que é a velocidade instantânea do corpo, que nesse caso é constante. A distância percorrida no caso em que a velocidade é uma função que varia ao longo do trajeto, que é o caso geral, será a integral desta função na variável tempo, como veremos a seguir.

A ideia principal por trás da construção da integral é a de área, que também está, implicitamente, incluída no cálculo da distância percorrida que acabamos de efetuar. De fato, observamos que a distância percorrida no caso da velocidade constante, entre os instantes de tempo $t_0$ e $t_1$ , é dada pela a área do retângulo limitado pelo eixo $x$ , pela reta $y=v_0$ , entre as retas verticais $x=t_0$ e $x=t_1$ , que é dada pelo produto de $t_1-t_0$ e $v_0$ , ou seja, $d = v_0(t_1-t_0)$ .

Para ilustrar isso, vamos supor que $v_0 = 2m/s$ e que, no instante $t_0=1s$ , o corpo está no ponto $d_0=1m$ . Então, a equação que nos dá a posição em função do tempo, conforme temos acima, é

$d(t) = d_0 + v_0(t-t_0) = 1 + 2(t-1) = 2t-1.$

Para $t=t_0 = 1s$ , $d(1) = 1m$ , e para $t=t_1=5s$ , $d(5) = 1+2(5-1) = 9m$ . Ou seja, o corpo percorreu a distância $2(5-1)m=8m$ entre os instantes $t_0=1s$ e $t_1 = 5s$ . E essa é a área do retângulo limitado pelo eixo $x$ ( $y=0$ ), pela reta que dá a velocidade ( $y=y_0 = 2$ ), e pelas retas verticais $x=t_0=1$ e $x=t_1=5$ , conforme a figura abaixo.

Para visualizar a situação em que a velocidade varia, veja a figura a seguir, onde a curva azul, dada por $y=v(x)$ , para cada $x=t$ , é o gráfico da velocidade. Para ver como definimos a função $v(x)$ , veja a nota ao final desse post.

Agora, se considerarmos a área da região delimitada pelo gráfico de $v(x)$ , o eixo $x$ , e as retas $x=1$ e $x=5$ , obtemos, novamente, o mesmo valor $8$ . Mais em geral, podemos calcular a área de uma região delimitada entre $x=1$ e $x=t$ , um ponto qualquer entre $x=1$ e $x=5$ , e obtemos a posição em função do tempo. Os gráficos da próxima figura fornecem os gráficos das posições dos dois corpos, em cada instante de tempo $(y=d_1(x)=2t-1$ em vermelho, para $v=v_0 =2m/s$ , e $d_2(x)$ em azul, para $v=v(t))$ .

Note que, como esperado, o segundo corpo, por ter uma velocidade maior do que o primeiro, para valores até $x=t=3s$ , avança mais rapidamente, mas após este ponto, perde velocidade e os dois acabam chegando no mesmo ponto quando $x=t_1=5s$ .

O fato de que ambos percorrem a mesma distância entre $t_0$ e $t_1$ decorre de que as áreas dadas entre cada um dos gráficos das velocidades e o eixo $x$ , nesse intervalo, são iguais. Isso é visualmente claro no gráfico das velocidades, pois o que se ganha no primeiro trecho, até $t=3s$ , para o segundo corpo, é perdido no segundo trecho, quando a velocidade fica menor do que $2m/s$ . Note a simetria do gráfico da velocidade variável em relação ao ponto $(3,2)$ , que decorre da definição de $v(x)$ (ver Nota ao final do post).

A função que nos forneceu a posição do segundo corpo foi calculada usando a integral da velocidade:

$d_2(t) = d_0 + \int_{t_0}^t v(x)dx = 1+ \int_1^t v(x)dx.$

A razão de utilizarmos a integral é que ela nos fornece a área da região estudada, que fornece a distância percorrida. Para entender essa afirmação, vamos lembrar como definimos a integral. Para isso, usamos aproximações por áreas de retângulos cuja base são subintervalos cada vez menores da forma $[x_i,x_{i+1}]$ , que subdividem o intervalo de integração, e cuja altura é dada pelo valor da função em algum ponto deste subintervalo. Ou seja, no caso do exemplo, pelo valor da velocidade neste ponto. Portanto, essa área é uma aproximação, como vimos acima no caso da velocidade constante, da distância percorrida no intervalo de tempo $[x_i, x_{i+1}]$ .

A soma destas áreas de pequenos retângulos é uma soma de Riemann para a integral, que aproxima a área da região e, no nosso exemplo, a distância percorrida pelo corpo. Ao tomarmos o limite das somas de Riemann quando o número de intervalos, que ficam cada vez menores, cresce para infinito, temos a integral, que é a área da região de interesse e, para nós, a distância percorrida no intervalo de tempo considerado.

Agora podemos enunciar o TFC, pois, se pensarmos que a velocidade é a derivada da posição no tempo, da velocidade obtemos a posição por integração e, derivando o resultado, devemos obter de volta a velocidade instantânea. Essa é a primeira versão do teorema:

Teorema Fundamental do Cálculo I – “A derivada da integral de uma função é a própria função”

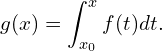Seja $f:(a,b)\longrightarrow\mathbb{R}$ contínua e $x_0\in(a,b)$ . Então, $f$ é integrável em em qualquer subintervalo $[c,d]\subset (a,b)$ e podemos definir a função $g:(a,b)\longrightarrow\mathbb{R}$ pela integral $\displaystyle g(x) = \int_{x_0}^x f(t)dt.$ Resulta que $g(x)$ é diferenciável para todo $x\in(a,b)$ e

$g^\prime(x) =\frac{d}{dx}\int_{x_0}^x f(t)dt = f(x).$

Observações: 1. A primeira parte do enunciado acima, de que uma função contínua é integrável, não é, usualmente, parte do enuncido do TFC, incluímos para que isso ficasse claro. Para esse resultado, ver T. Apostol, Cálculo I, Teorema 3.14. 2. A forma mais forte deste teorema pede apenas que a função $f(x)$ seja integrável e que seja contínua no ponto em que queremos derivar a integral. Nos pontos onde $f(x)$ não é contínua, em geral perdemos a diferenciabilidade de $g(x)$ , mas ainda obtemos que $g(x)$ será pelo menos contínua (exemplo: pense na integral de uma função degrau, com saltos em alguns pontos). Para os detalhes, ver T. Apostol, Cálculo I, Capítulo 5.

A versão acima do TFC tem uma consequência imediata, se lembrarmos que duas funções que possuem a mesma derivada diferem apenas por uma constante ( $\scriptstyle F_1^\prime(x) = F_2^\prime(x) \implies F_1^\prime(x)-F_2^\prime(x) = (F_1-F_2)^\prime(x) = 0 \implies F_1(x) - F_2(x) = K.$ ) A segunda forma do TFC garante a forma usual de calcular a integral de uma função $f$ , basta conhecer uma antiderivada (ou primitiva) de $f$ , isto é, uma função $F(x)$ tal que $F^\prime(x) = f(x)$ .

Teorema Fundamental do Cálculo II – “A integral definida de uma função é a diferença entre o valores final e inicial de uma antiderivada”

Seja uma função $f:(a,b)\longrightarrow\mathbb{R}$ tal que existe $F:(a,b)\longrightarrow\mathbb{R}$ diferenciável com $f(x) = F^{\prime}(x)$ . Então $f(x)$ é integrável em qualquer subintervalo $[c,d]\subset (a,b)$ e

$\int_c^d f(x)dx=\int_{c}^d F^{\prime}(x)dx = F(d)-F(c).$

Observação: trocando a variável de integração, obtemos a nossa função $g(x)$ da versão anterior usando a antiderivada:

$g(x) =\int_{x_0}^xf(t)dt =\int_{x_0}^x F^{\prime}(t)dt = F(x)-F(x_0).$

Demonstração do TFC I

Primeiramente, como observado acima, uma função contínua ser integrável é um resultado anterior ao do TFC e assumimos esse resultado aqui. Seguindo, temos, no enunciado, o ponto inicial para a integração, $x_0$ , e um ponto arbitrário, ponto final da integração, $x\in (a,b)$ . Considere um acréscimo $h>0$ , suficientemente pequeno, tal que ainda temos $[x,x+h]\subset (a,b)$ , o que é sempre possível obter (o que escreveremos aseguir, de fato, vale também para $h<0$ , basta considerar o intervalo $[x+h,x]$ ). Agora, pela aditividade da integral para subintervalos,

$\int_x^{x+h}f(t)dt = \int_{x_0}^{x+h}f(t)dt - \int_{x_0}^x f(t)dt = g(x+h)-g(x).$

Mas, como $f(t)$ é contínua, pelo Teorema do Valor Médio para integrais (T. Apostol, Cálculo I, Teorema 3.15), existe um ponto $\overline{x}\in [x,x+h]$ tal que

$f(\overline{x}) = \frac{g(x+h)-g(x)}{h}.$

Agora, como $\overline{x}\rightarrow x$ quando $h\rightarrow 0$ , usamos novamente a continuidade de $f(t)$ , obtendo

$\lim_{h \rightarrow 0}\frac{g(x+h)-g(x)}{h} = \lim_{\overline{x}\rightarrow x}f(\overline{x}) = f(x).$

Logo, $g$ é diferenciável em $x$ (o limite existe) e $g^\prime(x) = f(x)$ , como queríamos demonstrar.

Exemplo: se $f(x) =\cos(x)$ , como $F(x) = \textrm{sen}(x)$ satisfaz $F^\prime(x) = f(x)$ , a área entre o gráfico do cosseno e o eixo $x$ entre $0$ e $\pi/2$ é

$\int_0^{\pi/2} \cos(x)dx = \textrm{sen}(\pi/2) - \textrm{sen}(0) = 1-0 = 1.$

Exemplo: tome $f(x) = 1/x$ e $x_0 =1$ , e defina, para $x>0$ , a função $\displaystyle g(x) = \int_1^x f(t)dt = \int_1^x \frac{1}{t}\,dt.$ Pelo TFC I, $g(x)$ é uma função diferenciável para todo $x>0$ , pois $1/x$ é contínua para $x>0$ . Como sabemos, uma antiderivada para $1/x$ (para $x>0$ ) é $\log_e x = \ln x$ , o logaritmo natural.

Portanto, pelo TFC II, $g(x) = \ln(x)-\ln(1) = \ln(x)$ . De fato, é possível usar a definição de $g(x)$ a partir da integral de $1/x$ e provar todas as propriedades usuais do logaritmo natural, e então definir a exponencial de base natural (neperiana) pela inversa de $g(x)$ . Por exemplo, para a propriedade fundamental do logaritmo, $\ln(ab) = \ln(a) + \ln(b)$ , consideramos a aditividade da integral para subintervalos, obtendo

$\ln(ab) = \int_1^{ab}\frac{1}{t}dt = \int_1^a\frac{1}{t}dt + \int_a^{ab}\frac{1}{t}dt = \ln(a) +\int_a^{a b} \frac{1}{t}dt.$

Agora, basta fazer a substituição $t=au$ , e obtemos, completando a prova,

$\int_a^{ab} \frac{1}{t} dt = \int_1^b \frac{1}{au}adu = \int_1^b \frac{1}{u}du = \ln(b).$

Para mais detalhes, ver T. Apostol, Cálculo I, Cap. 6. O gráfico a seguir indica o valor da área da região entre $x=1$ e $x= 3$ , sob o gráfico de $1/x$ .

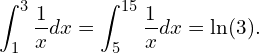Note que, pelo que acabamos de mostrar, se multiplicarmos o intervalo $[1,3]$ por uma constante, digamos, $c=5$ , obtendo o intervalo $[5,15]$ , temos $\displaystyle \int_1^3\frac{1}{x}dx = \int_5^{15}\frac{1}{x}dx =\ln(3).$ Tente interpretar geometricamente este resultado em um gráfico como o dado acima.

A maior parte das técnicas de integração dependem do TFC. Por exemplo, integração por partes (que seria a “inversa” da regra de Leibniz para derivação), integração por substituição (“inversa” da regra da cadeia), integração logarítmica, etc.

Desenvolvimentos avançados

O TFC apresenta versões mais avançadas, aplicáveis a funções de várias variáveis e a campos vetoriais. Os chamados “teoremas integrais vetoriais”, os Teoremas de Green, Gauss e Stokes, que são conteúdos do Cálculo de Várias Variáveis (Cálculo II), nada mais são do que versões do TFC naqueles contextos. O Teorema Generalizado de Stokes, que tem como objeto a integração sobre superfícies bem gerais, em qualquer dimensão, também é uma extensão do TFC, e suas consequências para a matemática mais avançada e suas aplicações à física moderna, incluindo a Teoria da Relatividade e outras áreas, são fundamentais.

Nota histórica

O Teorema Fundamental do Cálculo, ou melhor, a relação inversa entre derivada e integral, em outro linguajar e notação, acabou sendo formulado por Newton e por Leibniz, entre 1665 e 1676. A prioridade foi alvo de disputas, mas hoje se considera que ambos chegaram ao resultado de forma independente. Antecessores imediatos, como Fermat e Barrow, principalmente o último, chegaram perto de formularem a relação, mas, de fato, ainda não tinham as ferramentas apropriadas para isso.

Olhando a motivação acima, usando (A) distância percorrida e (B) velocidade (instantânea), que se relacionam de forma mais ou menos clara via derivada, de A para B, e integral, de B para A, parece estranho que isso tenha levado tanto tempo para ser formulado. O que ocorre, de fato, é que o próprio conceito de velocidade instantânea levou muitos séculos para ser formulado de forma apropriada, portanto, não havia, na própria mecânica (física), como estabelecer essa relação. Isso se deve ao fato que os gregos, quando começaram a formular os conceitos matemáticos fundamentais, esbarraram na ideia de processos infinitos, que é o que se precisa para formular o conceito de velocidade instantânea, de onde vem a própria ideia de derivada. Isso decorreu dos chamados “paradoxos de Zeno“, que derivavam aparente absurdos (como a impossibilidade do movimento acontecer) a partir de construções que envolveriam “infinitas” etapas. Eles já tinham uma boa ideia de como calcular áreas, mas sempre de forma estática, sem pensar na ideia de relacionar isso ao movimento, como Newton, principalmente, acabou fazendo e, então, utilizando para formular a relação entre derivada e integral. Leibniz o fez de forma um pouco diferente, ma acabou chegando aos mesmos resultados.

As formulações atuais, apresentadas acima, no entanto, são de período mais recente, sendo que as próprias definições de derivada e integral que hoje utilizamos, envolvendo o conceito de limite, só foram introduzidas no século 19, por Cauchy e Riemann. Para detalhes sobre a história do Cálculo, ver Carl B. Boyer, The History of the Calculus and its Conceptual Development, Dover.

Nota: como foi definida a função $v(x)$

No exemplo de velocidade variável, para obter uma função simétrica pelo ponto $(3,2)$ e, assim, tal que a área sob seu gráfico, entre $x=1$ e $x=5$ , fosse igual à área do retângulo dado pela função constante $v_0 = 2m/s$ , começamos com o monômio $p(x) = x^3$ . Em seguida, separamos as raízes (que para $p(x)$ seriam todas iguais a zero) de forma simétrica à origem, colocando-as no valores $x=-2$ , $x=0$ e $x=2$ : $q(x) = (x+2)x(x-2)= x(x+2)(x-2)$ . Os gráficos de $p(x)$ e $q(x)$ são simétricos em relação à origem, pois elas são funções ímpares $(f(-x) = -f(x))$ :

Agora, fazemos três transformações usuais de funções. Primeiro, reduzimos a amplitude da variação, dividindo a função $q(x)$ por $4$ : $r(x) = x(x-2)(x+2)/4$ . Note que essa função ainda é ímpar, ou seja, seu gráfico é simétrico pela origem. Em seguida, transladamos o gráfico de $r(x)$ de três unidades para a direita, subtraindo $3$ da variável: $s(x) = (x-3)(x-5)(x-1)/4,$ que coloca as raízes em $x=1$ , $x=3$ e $x=5$ . Essa função é simétrica pelo ponto $(3,0)$ . Agora, para que o gráfico varie em torno da reta $y= 2$ , somamos duas unidades ao valor da função, transladando o gráfico em duas unidades para cima, obtendo, finalmente, $v(x) = 2+ (x-1)(x-3)(x-5)/4$ , cujo gráfico está no corpo do post e é simétrico em relação ao ponto $(3,2)$ , como queríamos. Para treinar, esboce os gráficos de todas as etapas da definição de $v(x)$ .

Talvez você goste também

Roger Penrose ganha o Prêmio Nobel de Física

O que Richard Courant disse sobre o Cálculo

Deixe um comentário Cancelar resposta